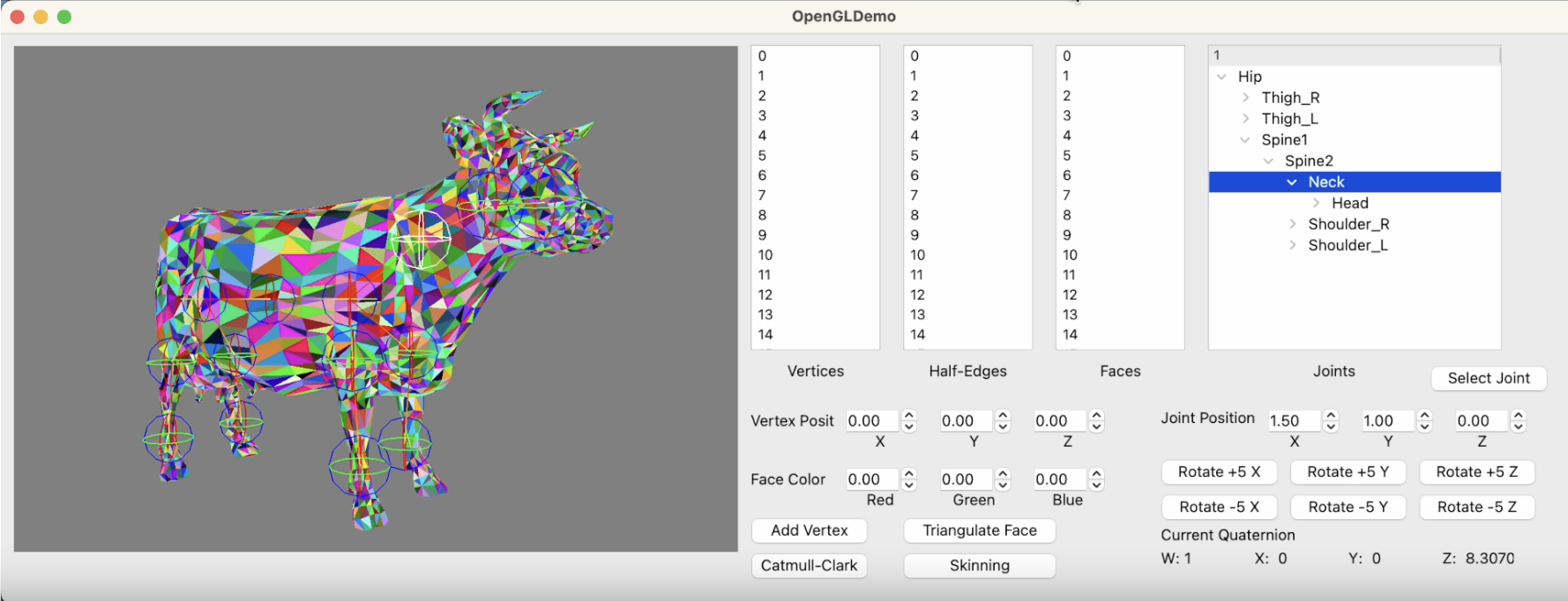
Micro Maya
This project was 3-4 week task assigned in CIS 4600/5600, where I created a mini version of the 3D modeling software Maya. There were three main challenges to this project: creating the data structure used to represent 3D meshes, performing subdivisions to an arbitrary mesh structure, and applying a skeleton to a mesh to allow transformations to the mesh.
C++
GLSL
Qt
Half Edge Mesh
The first step in creating Micro Maya was determining how to represent 3D meshes so that they could be transformed and distorted easily. Each mesh structure has three main parts - vertices, edges, and faces. Because my goal was to create a mini version of Maya, I wanted to make basic mesh editing functions availabe, such as moving vertices/edges/faces and changing their colors.
To do this, I chose to represent meshes using a half edge data structure. Half edges are directed edges that frame a face. Each half edge stores a pointer to the face directly left of it, the next half edge in the ring of edges, its symmetric half edge, and the vertex between itself and the next half edge. This information allows for more convenient traversal around the data structure, making operations like edge splitting and subdivision easier. I took advantage of this half edge data structure to implement triangulation.
To the right is an example showing the process of triangulation on the face of a dodecahedron.
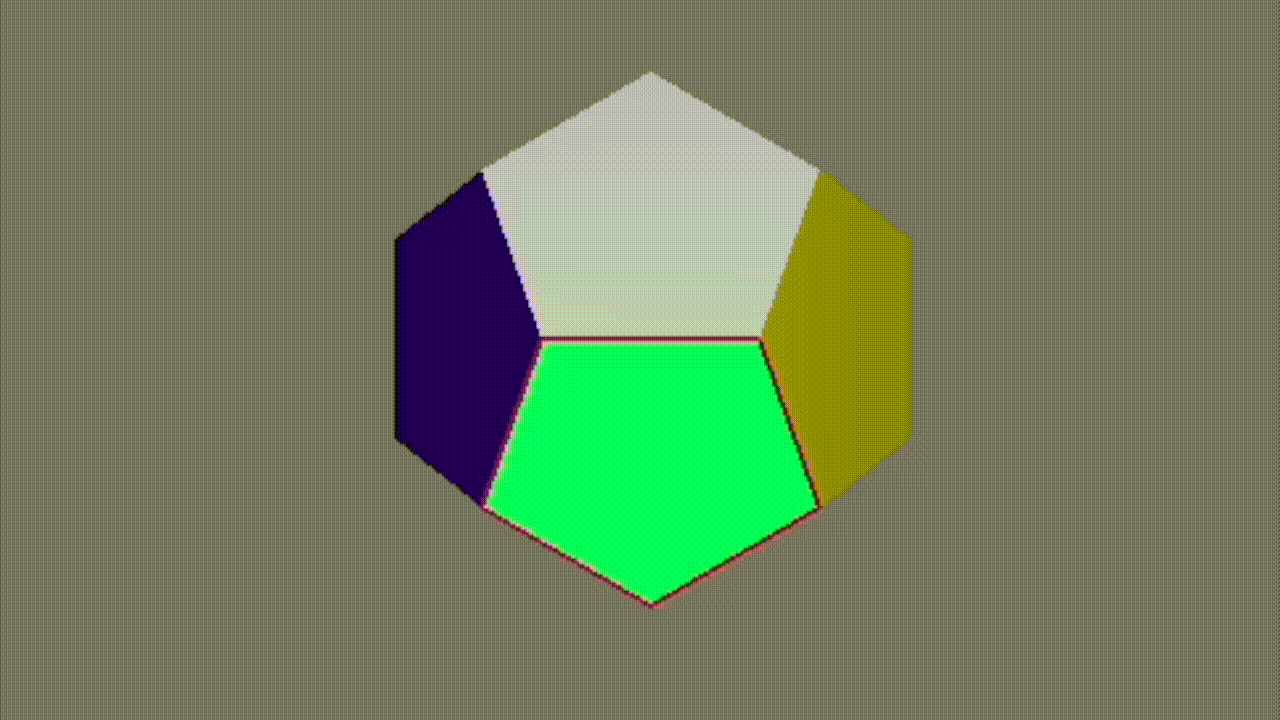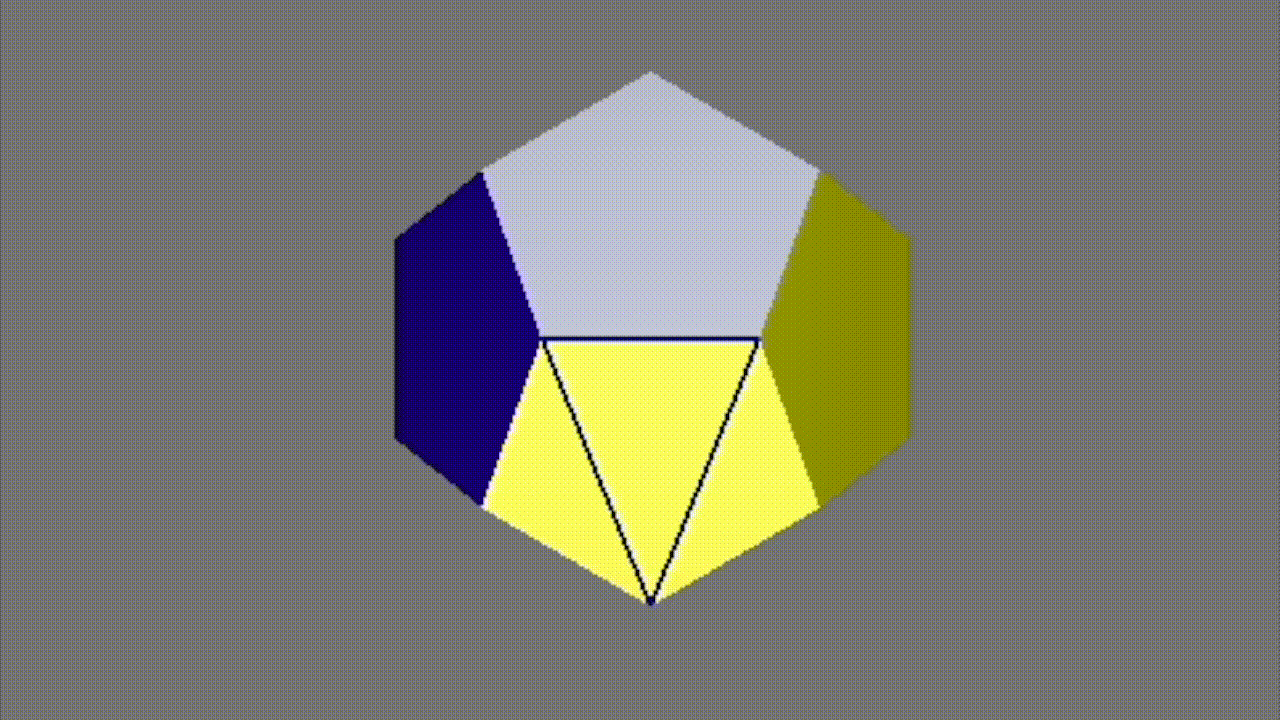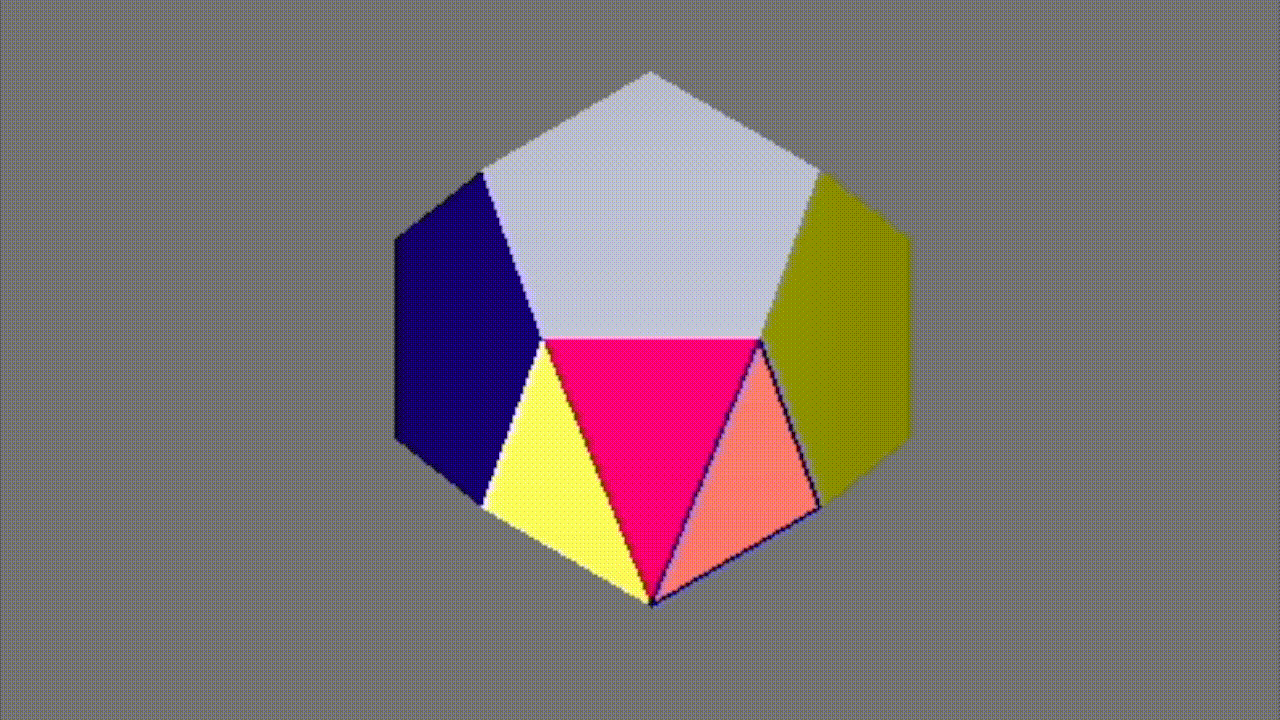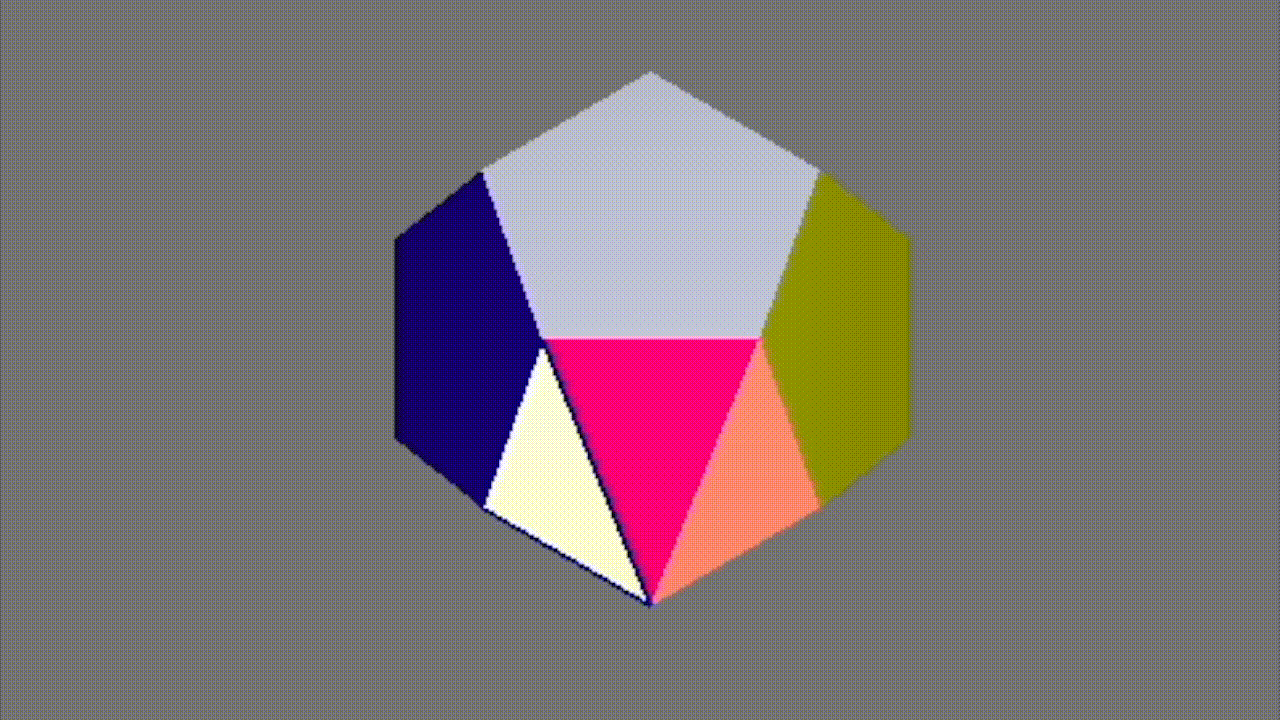
In the demo, I first select the front face of the dodecahedron. (The color of the face transitions from green to yellow to illustrate its shape before triangulation). Then, after triangulation, the pentagon becomes split so that the face is now composed of triangles. This is done by creating two new faces (for a total of three triangular faces) and four new half edges. Because our half edge data structure allows for easy traversal, we can fix the pointers of our half edges easily and successfully split the face into three.
Catmull-Clark Subdivision
Another nice operation of Micro Maya is Catmull-Clark Subdivision, a method of smoothing a mesh. Catmull-Clark works by taking the centroid of each face, computing the midpoint of each edge in the mesh, and then using these values to smooth the original vertices. Each face in the initial mesh gets split into a number of quadrangle faces equal to the original number of vertices.
Below is a demonstration of a series of three Catmull-Clark subdivisions, each one bringing the initial cube closer to a sphere.




Skeletons & Skinning
My favorite part about this project was attaching a skeleton to a 3D mesh and using it transform the mesh. Each skeleton is composed of a hierarchy of joints. When loaded in, a skeleton can be moved around without affecting the mesh. However, the skeleton can be attached to the object by clicking the 'Skinning' button, and then any transformations applied to the joints will be applied to the mesh as well.